カノジョに追い付きたい
みなさん、こんにちは!
B-CHANです。
先日経験した、不思議な話を聞いてくださいよ!
ボクが道を歩いていたら、ボクのカノジョがボクの前方100メートルのところを歩いているのを見つけました。
ボクはカノジョに追いつこうと思って、カノジョの歩く速さの2倍の速さで、カノジョの方に向かって進みました。
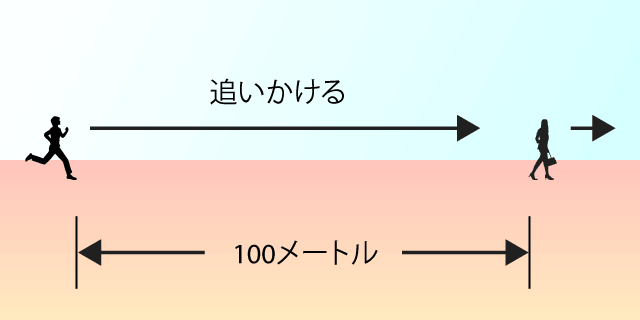
ボクが100メートル進んで、カノジョがいた場所に到着すると、カノジョはすでに50メートル先にいました。

そりゃそうですね。ボクはカノジョの2倍の速さで進んでるんですから、ボクが100メートル進んだら、カノジョは50メートル進んでいるわけです。
そこで引き続き、ボクは同じペースで進みました。
ボクが50メートル進んでカノジョがいた場所に到着すると、カノジョはすでに25メートル先にいるのです。
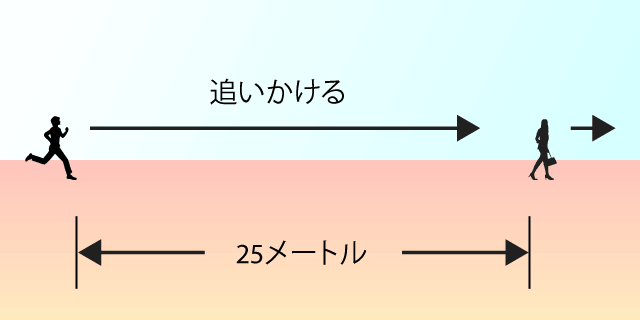
ボクはめげずに25メートル進みました。するとカノジョは12.5メートル先にいます。
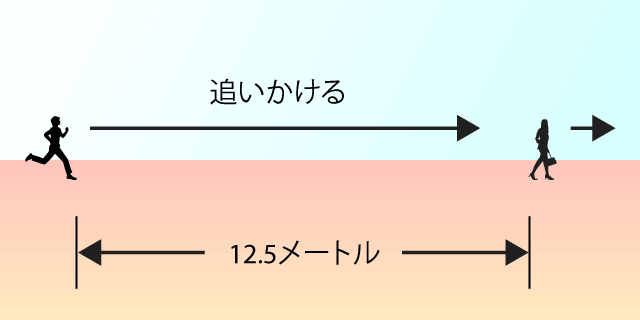
ボクはさらに追いかけるために、そこから12.5メートル進みました。するとカノジョはもう、6.25メートル先にいます。
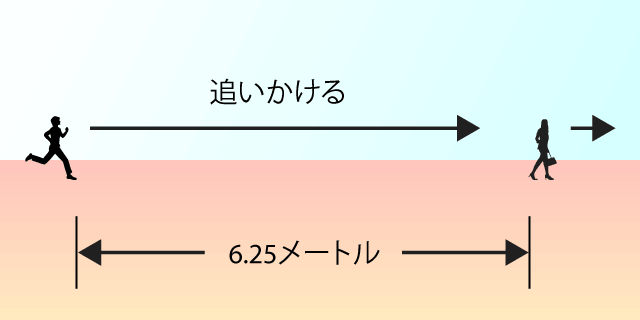
そして、ボクがそこから6.25メートル進むと、カノジョは3.125メートル先にいるのです。
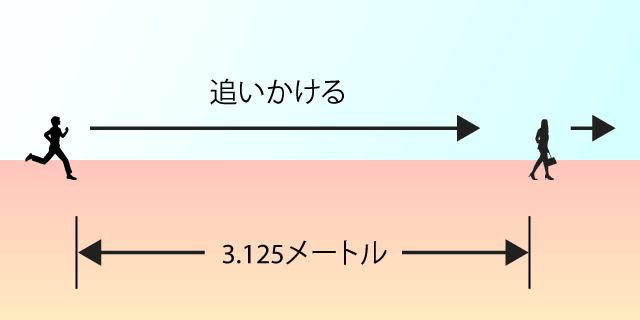
以下、これの繰り返しでした。
ボクがカノジョのいた地点に到達すると、カノジョはすでにそこにはいなくて、先に進んでしまっています。
これが無限に続くわけです。
ボクは考えました。
「これって永遠にカノジョに追いつけないってことだ。」
仕方なくボクはカノジョに追いつくのをあきらめました。
いかがですか?
みなさんはこんな経験ありませんか?
何だかとても不思議な感じがしますが、論理的には矛盾してないんですよね。
アキレスと亀
実は上の話は作り話です、当たり前ですが。ボクのカノジョって誰だよ!
それはさておき、これは、ゼノンのパラドックスにおける、有名な「アキレスと亀」の話のアレンジです。
足の速いアキレスと、足の遅い亀が競走することになり、ハンディキャップとして、亀のスタートラインをアキレスより前方にしました。
スタートし、アキレスが 亀のいた場所に到達すると常に亀はアキレスより前方にいます。
つまり、アキレスは永遠に亀に追いつかないということになってしまいます。
理論的には間違っていないんですが、数学的には、これは極限に収束しますね。
アキレスと亀の間隔、すなわちボクとカノジョとの間隔はどんどん狭くなっていき、ある地点で究極的にゼロに近づきます。これが極限値ですね。
数値上は無限に続くことでも、現実には割り切れます。
例えば、長さ1メートルの木を3等分すると、ひとつの長さは、
0.33333333333……メール
と永久に割りきれませんが、実際には3等分で切ることは可能です。
長さ3メートルの木を3等分すると、ひとつの長さは1メートルになるのと同じですね。
論理的には無限でも、現実には割りきって存在できる事象です。
世の中にはこういう問題を研究している人たちがたくさんいて、とっても面白いです。
次は、モンティ・ホール問題をわかりやすく書いてみたいんですが、ボク自身が噛み砕いている最中です。
期待しないで待っててください。
関連記事
警察が隠れて交通違反を取り締まる必要がある理由 - 非天マザー by B-CHAN
努力すれば報われる? 必要条件と十分条件の違いを学ぼう - 非天マザー by B-CHAN
牛乳を飲む人は寿命が短いという調査がおかしい理由に気付きましたか? - 非天マザー by B-CHAN
「エリートの大半は早起き」と聞いて早起きするのが間違いである理由 - 非天マザー by B-CHAN
「おいしい話は他人に教えない」と考える人が失敗する理由 - 非天マザー by B-CHAN