カレーが好きな人の命題
今日も、論理的思考の基礎の基礎をやってみましょうか。次の図を見てください。
とある学校のとあるクラス(Aクラスとします)に生徒が10人いて、10人ともカレー好きとします。
つまりAクラスの生徒は全員、カレーが好きです。
さて、この学校を訪れた人が、学校にいるとある生徒に、カレーが好きかどうかを尋ねたところ、その生徒が、カレーが好きだと答えたとします。
すると、その人は、
「キミはAクラスか。」
と推測しがちになります。
Aクラスの生徒は全員がカレー好き。
↓
そして今、目の前の生徒はカレー好き。
↓
つまり、この生徒はAクラスである可能性が高い。
となるわけです。
こう考える人は多いと思いますが、これ、大間違いです。
逆は必ずしも真ならず
命題
「Aクラスの生徒ならば全員カレー好き」(AならばB)
↑
↓
命題の逆
「カレー好きな生徒ならばAクラス」(BならばA)
学校で学んだ人もいると思います。
命題「AならばB」の逆は「BならばA」ですね。
そして、とある命題が成り立っても、その逆は正しいとは限りません。
次の図を見てください。
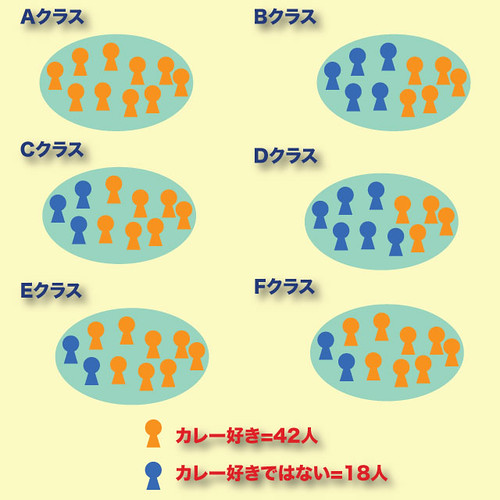
この学校にはAからFまで6クラスあり、各クラスには生徒が10人ずつ、合計60人います。
カレーが好きな生徒(オレンジ色)は全体で42人。
カレーが好きでは無い生徒(青色)は全体で18人。
この図を見ればわかるように、カレーが好きな生徒(42人)のうち、Aクラスに所属しているのは10人のみ。
つまり確率は四分の一もありません。
この学校でカレー好きな生徒に出会った場合、その生徒はAクラスでは無い確率のほうが圧倒的に高いわけです。
「カレー好きだからAクラス」は間違いである可能性の方がずっと大きいのです。
Aクラスの全員がカレー好きかどうかは全然関係無いわけです。
にも関わらず、「AならばB」のときに「BならばA」だと考えてしまう人が多いんですね。
整形
なんでこんな話になったかというと、整形の話題からです。とある人が久しぶりに会うと、顔が変わっていた、
だから、整形したんじゃ無いか、と言った人がいたからです。
上記のカレーの例と全く同じです。
命題「整形した人は全員顔が変わる」(AならばB)
逆「顔が変わった人は全員整形だ」(BならばA)
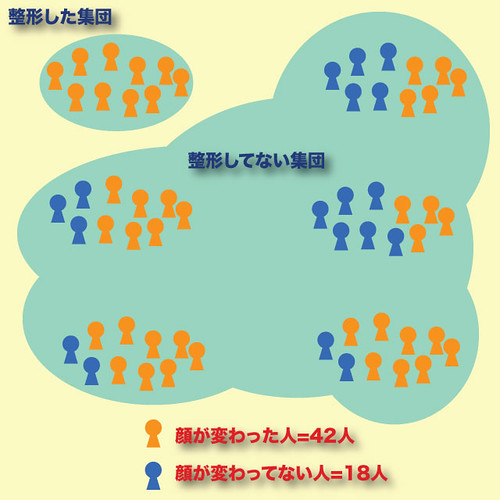
当然、命題が正しくても、逆が成り立つとは限りません。
つまり整形しなくても顔が変わる人はたくさんいます。
だから、顔が変わったから整形したと疑うのは根拠にならないということです。
むしろ、その疑いをかけて事実と異なっていた場合、疑いを掛けられた方も傷つく事があるので、そういう無根拠な過ちは犯さないように気をつけましょう、と言うことですね。
ま、ボクは整形なんてどっちでもいいですけど。
関連記事
大きな事件に目を奪われて判断を誤るリスク
択一式アンケートの恐ろしさと数字のからくりと世論
思い込みという誤解