暗記では無く考える事が大事
小学生レベルの話ですが、小学生レベルだからと言ってバカにできない話です。あなたは、なぜ、三角形の面積を求める公式が、
三角形の面積 = 底辺の長さ × 高さ ÷ 2
なのか、きちんと説明できますか?
長方形の面積
まず、長方形の面積を考えます。これは簡単で、
長方形の面積 = 横の長さ × 縦の長さ
です。
なぜそうなるかは次の図を見れば明らかです。
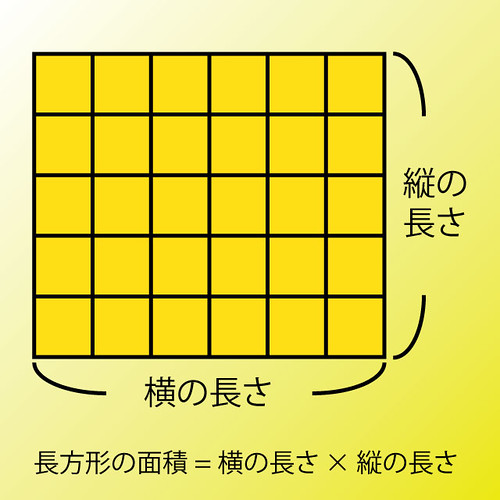
マス目が横に6個並んでいますよね。
それが5段あります。
6個が5段あるので、
6 × 5 = 30
です。
もし単位が、cmなら、
6cm × 5cm = 30平方cm
ですね。
横の長さ × 縦の長さ が長方形の面積になるわけです。
三角形の面積を導き出す
次の図を見てください。三角形の面積の公式です。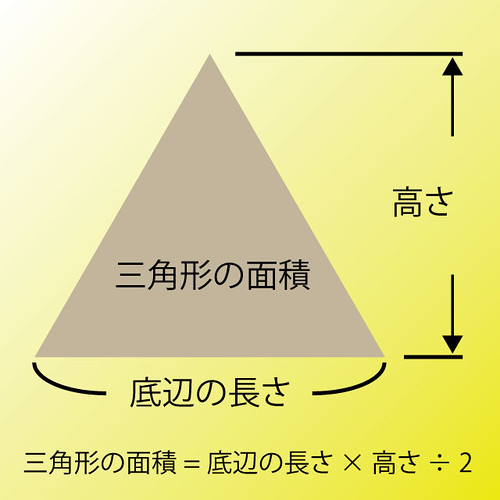
さて、なぜ三角形の面積の公式は、
三角形の面積 = 底辺の長さ × 高さ ÷ 2
なんでしょうか。
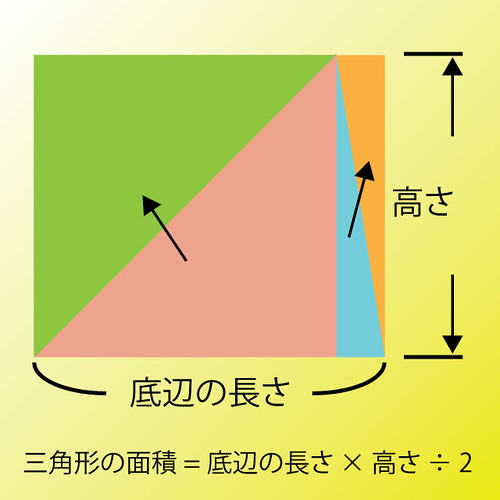
それには次の図を見てください。
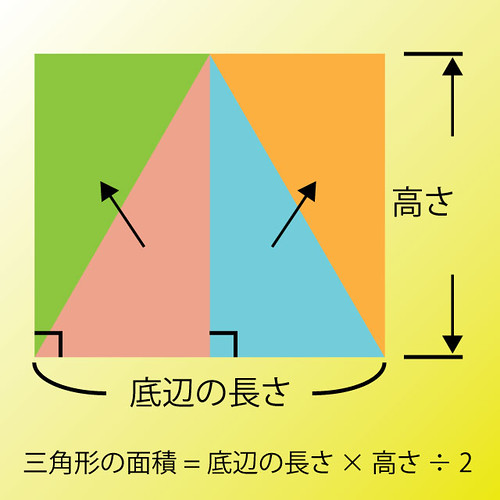
まず、元の三角形を垂直な線で2つに分割します。
ピンク色と水色の部分です。
そしてピンク色と同じ大きさで同じ形の三角形を180度回転してくっつけます。緑色の部分です。
同じように水色の三角形と同じものをくっつけます。オレンジ色の部分です。
これで、
元の三角形の、
ピンク色
水色
が、
新しい長方形である、
ピンク色
水色
緑色
オレンジ色
になりました。
ピンク色と緑色
は同じ面積、水色とオレンジ色は同じ面積なので、新しい長方形は、元の三角形のちょうど2倍の面積になりますね。
すると、この新しい長方形の面積がわかりますよね。
最初にやったように、
長方形の面積 = 横の長さ × 縦の長さ
なので、この図で言えば、
長方形の面積 = 底辺の長さ(横の長さ) × 高さ(縦の長さ)
ですよね。
そして、いま書いたように、この長方形の面積は、元の三角形の2倍の面積なので、三角形の面積は、この長方形の面積を2で割ればいいわけです。
つまり、
三角形の面積 = 底辺の長さ × 高さ ÷ 2
はい、見事に、三角形の面積の公式になりました。
どんな三角形でもOK
別の三角形でもやってみましょう。理屈はまったく同じです。
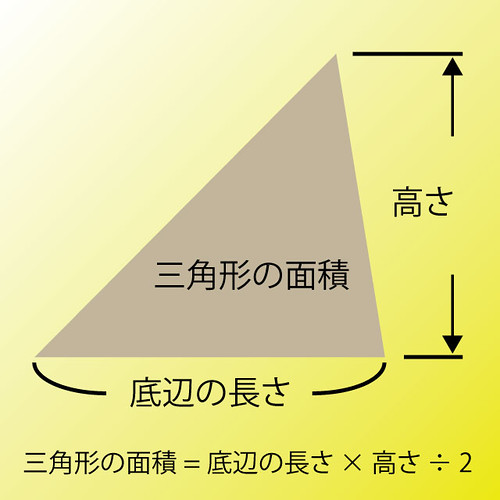
では、次の三角形はどうでしょうか?
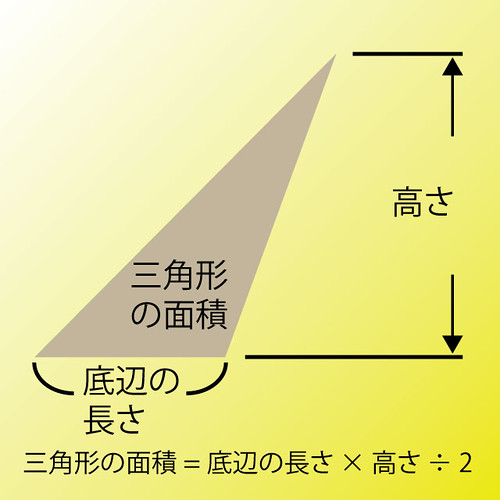
この場合、そのままでは、さっきのやり方ができません。
でも簡単。
次のように、赤い三角形を足してください。
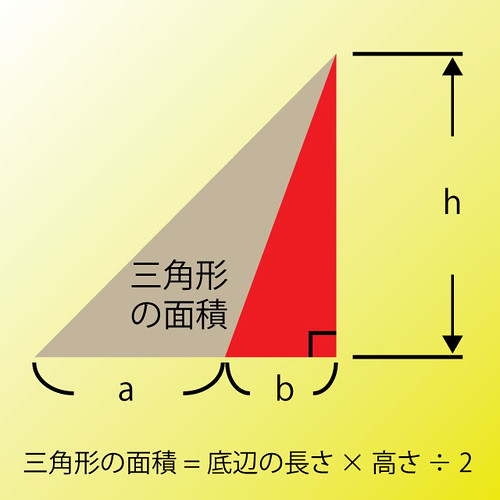
元の三角形と赤い三角形を足して、ひとつの大きな三角形と見ることができます。
この大きな三角形の面積から、赤い三角形の面積を引けば、元の三角形の面積ですよね。
大きな三角形と赤い三角形の面積はそれぞれ、さっきのやり方でわかります。
大きな三角形は、
底辺の長さ(a + b) × 高さh ÷ 2 …… X
赤い三角形は、
底辺の長さb × 高さh ÷ 2 …… Y
なので、元の三角形の面積は、XからYを引けばいいですね。
X - Y = (a + b) × h ÷ 2 - b × h ÷ 2
です。
これを整理すると、結局、bの項が消えてしまうので、
元の三角形の面積 = a × h ÷ 2
これは、元の三角形の、
底辺の長さ × 高さ ÷ 2
って事ですよね。
こんないびつな三角形でも、この公式で面積が出るって事です。
めでたしめでたし。
知っていることは偉くも何とも無い
三角形の面積を求めるときに、毎回こんな面倒な事は考える必要は無く、三角形の面積 = 底辺の長さ × 高さ ÷ 2
という公式にあてはめれば良いことがわかりました。
学校のテストでも、公式を使って解く問題が出されるでしょう。
しかし、その問題を解いて、テストで同じ点数を取った人が二人いたとしても、一人は公式を暗記しているだけで、もう一人は、上記の説明ができる人なら、能力は全然違います。
これは、学校のテストでは頭の良さを測るのに限界がある理由です。
例えば、東京タワーを見たことも聞いたこともない、どこかの外国の人に、東京タワーの色を尋ねたとします。
その人は、どんなに天才でも東京タワーの色を答えることができません。
逆に東京タワーを知っている人なら、頭が良くても悪くても東京タワーは赤いと答えることができます。
つまり、知っているか知らないか、それだけの事です。
ボクが受験生の頃、関西での私大の雄である関関同立の某大学を受験したんですが、その時の国語の問題で、
- 漢字の読み方
- 漢字の画数
ボクは正直、あ然としました。
大学生になるための頭の良さを問うべき試験問題で、何の応用性も無い漢字の読み方を問う事についてです。
例えば、三角形の面積の公式なら、仮に忘れてしまっても、上で書いたように、自分で考えて導き出すことが可能です。
しかし、漢字の読み方には基本的には応用力は不要で、単にたまたま知っているかどうかです。
そんな入試問題を作っていると、頭は良くなくてもたまたま知っている人が合格してしまうことになります。
そして、その大学を卒業すると、
高学歴 = 頭が良い
という勘違いが生じるわけです。
これは採用する企業に取ってもダメージになりかねないと思うんですよね。
高学歴だからと言って採用してみたけど、実は非常に思考力が低かった……。
ボクの母校である阪大のその年の英語の入試問題で、こんなのがありました。
「あなたが地球で一番最初に宇宙人に会った人です。宇宙人とどんな会話をするか、50語以内の英語で書きなさい。」
上記の漢字の読み方を出題した入試問題との格差に驚きました。
単に偏差値が高いという、つまらない視点で判断するのではなく、きちんと内容で判断すると、並みの大学では無いことがわかって安心しました。
難しい単語を使う必要なんて無いわけです。それは知識の問題なので。
自分の頭で考えて文章を組み立てて、それを短いながらも英語で論述する、英文法の知識があるのは当然で、まさに思考力と応用力が問われる問題でした。
他には例えば東大の日本史でも論文的な問題が出題されますし、京大の英語でも論文に近いです。
決して暗記の知識だけを問う問題は出ません。
日本の国際競争力が落ちてきているのは、日本人がそういう応用力の不要な環境で暮らしている間に、発展途上国の人たちが、知識はもとより、思考力、応用力、行動力を発揮してきているからだと思っています。
日本が再び相対的な力を奪還するためには、入試問題で漢字の読み方を問う大学は淘汰されていく必要があり、そういう社会から脱却する必要があるんじゃないかなあ、と感じました。
表面的な偏差値の高さで判断せず、きちんと中身で判断する、それは物事にも人物にも当てはまる、このブログでもずっと言い続けてきました。
この記事の趣旨が、三角形の面積を自分で導けるようにしよう、では無いことがわかってもらえたでしょうか。
関連記事
ものぐさな人でも有利に運用できる理由を書きます。ドルコスト平均法。面白いです。
宝くじと期待値と大数の法則
本質で物事を考えよう、命を守るために(おかしな世の中をつぶやくシリーズ)