小学生なので方程式は使えない
みなさん、こんにちは!
B-CHANです。
インターネットで昨日あたりから、
「大きさの違う3つの正方形を並べた形の面積を答えよ。」
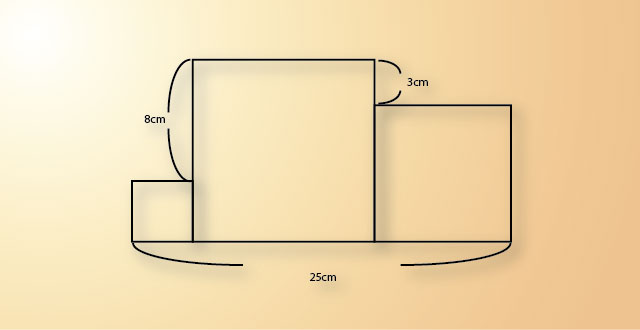
という出題が話題になっていますね。
塾講師や家庭教師経験豊富で、頭の体操大好きなボクは、この手の問題を見ると、ついつい取り組んでしまうんですが、今回はちょっと困りました。
なぜなら、この問題が小学校4年生の算数の問題だからです。
方程式を使った解答
実は、この問題、方程式を使えば簡単に解けます。
真ん中の一番大きな正方形の一辺の長さを、x、と置けば、
左側の正方形の一辺の長さは、x-8、
右側の正方形の一辺の長さは、x-3、
です。
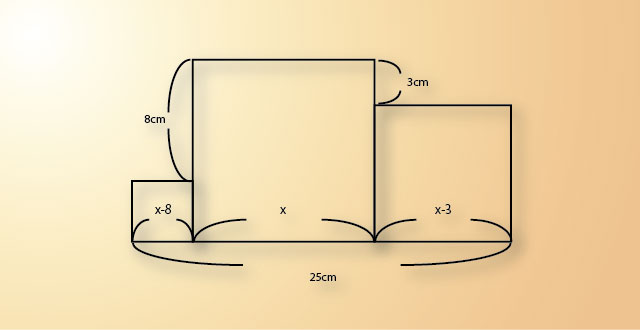
x + (x-8) + (x-3) = 25
x=12
となります。
真ん中の正方形の一辺の長さは、12cm、
左側の正方形の一辺の長さは、4cm、
右側の正方形の一辺の長さは、9cm、
よって、
真ん中の正方形の面積は、12cmの2乗=144c㎡、
左側の正方形の面積は、4cmの2乗=16c㎡、
右側の正方形の面積は、9cmの2乗=81c㎡、
合計では、144c㎡ + 16c㎡ + 81c㎡ = 241c㎡
これが答えです。
方程式を使える中学生以上なら簡単に解ける問題なんですね。
でも、小学4年生たちは方程式を知らないので、方程式無しでこの問題を解く必要があります。
これがこの問題を難しくしているんですね。
小学生の知識での解答
図形問題の鉄則は線を補完すること。
この問題でも、このままだと解けないので、真ん中の正方形と同じ大きさの正方形を左右にも並べてみます。
赤い線で示しました。
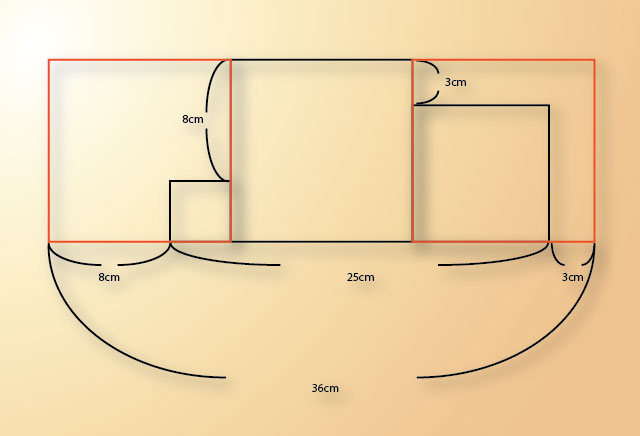
これで同じ正方形が横に3つ並びました。
3つ並べれば、25cmの左に8cm、右に3cmが加わることがわかるので、全体では36cmになりますね。
これによって一番大きな正方形の一辺は、36cm ÷ 3 = 12cm だとわかりました。
よって、左側の正方形の一辺は、12cm - 8cm = 4cm、右側の正方形の一辺は、12cm - 3cm = 9cm、だとわかります。
これで下図のように答えの241c㎡が求められます。
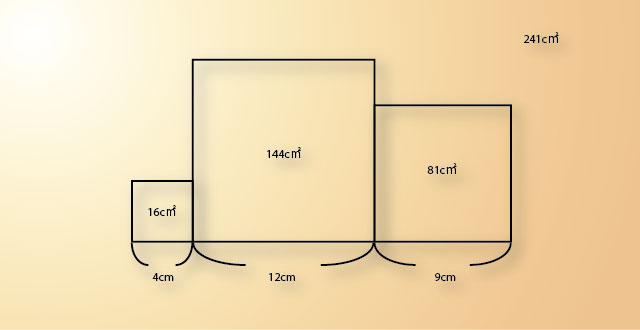
この解き方をやりながら思ったのは、小学生のやり方は上記の方程式の理論と全然違うってことです。
最初ボクは、図で描いても、結局は方程式のやり方を図にしただけになるだろうと予想していました。
でも違っていました。
方程式の方は25cmという長さがキーとなりましたが、小学生のやり方は36cmがキーになります。
なので、同じ答えを導くのに、ぜんぜん違うアプローチを使うんですよね。
効率化の結果の思考力の低下
大人になると効率が求められることが多いので、このような問題を解く時はほとんどの人が方程式を使うと思います。
でも、ぜんぜん違うアプローチも存在します。
もしかしたら、この問題は小学生には難しくないのかもしれません。
効率の良い方法に慣れてしまうことで、ホントは簡単な事ですら難解にしてしまう。
そんな感想を持ちました。
日常の仕事でも生活でも常に、違うやり方は無いだろうかという意識を持っていたいですね。
そうすれば新しい発見があるかもしれません。
